In a two-dimensional plane, all living beings are considered as points. Two sheep are at the same point, which is 1 unit away from the wolf. The wolf’s speed is 1, and the sheep’s speed is 0.5. All creatures move simultaneously and continuously with instantaneous reactions. When the distance between the sheep and the wolf is 0, the sheep will be eaten. The wolf wants to minimize the time it takes to eat both sheep, while the sheep want to maximize this time. How should they move? And how much time does the wolf need to eat both sheep?
Translated from https://mp.weixin.qq.com/s/qysNm-VDBbPCL6l3WdtnKA
The wolf wants to catch the two sheep with minimum time cost. It runs toward the nearest sheep. After catching the first, It runs to the other sheep.
Let sheep A be closer to the wolf W than sheep B.
sheep A runs in the direction that maximizes ||WA|| + ||AB||. The direction splits ∠WAB evenly.
sheep B runs away from sheep A.
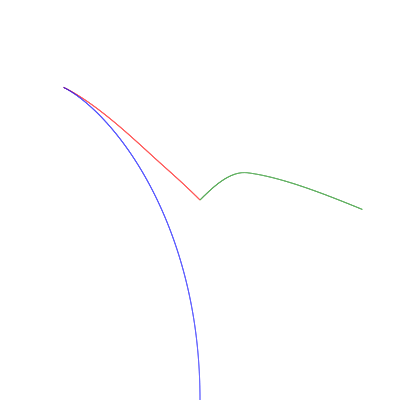
Result from page racing.html
greedy strategy: 
total time: 5.003527201219288.
source code: greedy.js
If we know final locations (sheep A at F, sheep B at G) when sheep A is caught, then sheep A should choose direction that maximizes ||WA|| + ||AG||, while sheep B should run away from F and keeping ||WB|| ≥ ||WA||.
Result from page racing.html
tricky strategy: 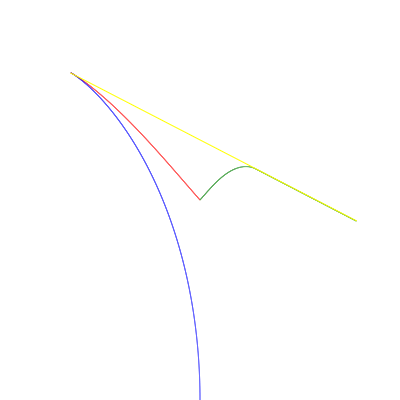
total time: 5.037744142633788.
source code: tricky.js